Why Learn Trigonometry?

We have spoken a great deal about visualizing functions and trigonometry concepts, but let's take a step back for a moment and see the bigger picture.

Trigonometry did not click for a long time for me.  To this day, I am still relearning the simplest ideas and seeing them in new ways.  The unit circle is nice to learn, as it gives us a great foundation and the number 1 is easy to work with, but there is another fascinating parallel we can make.

The height of the human body is roughly equal to our arm span.  If we draw a square and a circle around a human figure, we can see two very distinct relationships, and this is where ancient mathematicians discovered a great deal of their insight and wisdom.

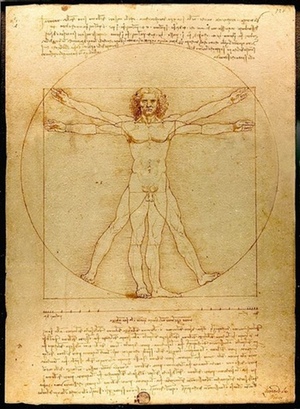Vitruvian Man
Retrieved from https://en.wikipedia.org/wiki/Vitruvian_Man#/media/File:Da_Vinci_Vitruve_Luc_Viatour.jpg

If we stand with legs together and arms straight out, we form a square, and if we angle our legs and arms, we maintain the same relationship, but since we are moving a constant radius, we are moving our limbs along a circle.

If you have trouble memorizing the trig functions in the way we discussed earlier, perhaps we can visualize them another way.

Pretend we are in the middle of a dome.

Now pretend someone has built a wall at the edge of our dome.  It would appear like this:

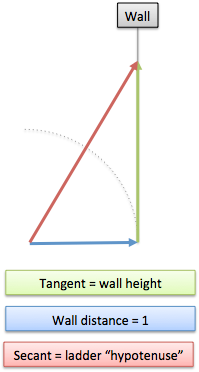Wall Example
Retrived from http://betterexplained.com/wp-content/uploads/trig/trig-wall.png

In this example, we can visualize tangent and secant in a new way.  Suppose the wall is blocking our vision.  To climb the tangent wall (green), we'll build a secant ladder (red).  Now you can SEE, CAN'T you?  Get it?  Secant?  Tough crowd...

I didn't come up with it, but thank Kalid Azad at http://betterexplained.com/articles/intuitive-trigonometry/.  I highly recommend reading this site for a more thorough explanation.

Now that we have seen tangent and secant, cosecant and cotangent are not far off.  Instead of a wall, let's pretend a ceiling was built instead.  Imagine that it extends outward beyond the edge of the dome.

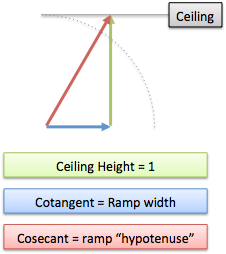Ceiling Example
Retrieved from http://betterexplained.com/wp-content/uploads/trig/trig-ceiling.png

In this example, the height of the ceiling is the radius of the dome (green).  This could easily have been built at the origin, but placing it outward better illustrates the red ramp, which is the cosecant.  If we have a given angle, the cotangent is the length of the base of the ramp, and the cosecant is the length of the ramp itself, rising toward the ceiling.

When we put both of these drawings together, we get a brilliant illustration of all the trig functions relating to one another, all forming similar triangles which can easily be solved with simple ratios.

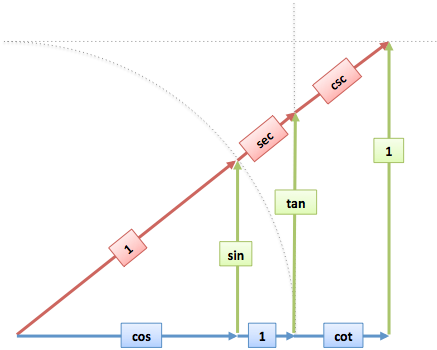Combined Graph
Retrieved from http://betterexplained.com/wp-content/uploads/trig/trig-overall.png

From here, we can actually re-derive the trig identities we learned last time in a much simpler way than memorizing.  Take the blue segment, the green segment, and the red segment connecting the two, and we form all three of the Pythagorean Identities.

Consider the original Pythagorean Theorum:
a^2 + b^2 = c^2

cos^2(x) + sin^2(x) = 1

1 + tan^2(x) = sec^2(x)

cot^2(x) + 1 = csc^2(x)

It's pretty amazing when we put them all together in this way.  Trig functions can be derived in so many ways because triangles and circles are so closely related.

Sources: 

Kalid, Azad. How To Learn Trigonometry Intuitively. Retrieved November 30, 2015, from http://betterexplained.com/articles/intuitive-trigonometry