As we dive into Trigonometry this year, we are going to be met with a ton of new concepts. The unit circle is one such concept which will become extremely useful in our class. It is so useful, in fact, that it will continue to be used throughout calculus and beyond.
Some of these concepts seem strange to work with at first; maybe even intimidating. Instead of polygons, we start seeing curved functions like sine, cosine and tangent, which suddenly seem a lot more difficult to work with. The circle is an easy and familiar shape though.
We have a good handle on working with rectangles and right triangles. The unit circle is really no different: we are just looking at right triangles from a new perspective. The definition of a circle is all points equidistant from its center, with the distance being r (the radius). We know 2πr is the circumference of any circle, and the unit circle is simply a circle with r=1, giving us a circumference of simply 2π.
When we draw the unit circle at the origin (0,0) it is divided into four 90-degree quadrants.
| Unit Circle: http://etc.usf.edu/ |
The beauty of the unit circle is you only need to memorize the first quadrant. We have 5 angles to work with, which are 0°, 30°, 45°, 60°, and 90°. We can trace a right triangle over all of these.
Lets look at 0°. On a coordinate plane, we simply get the point (1,0) - this is because the radius (1) is going straight in the x direction. Easy, right? We can always think of cosine as the "x" value and sine as the "y" value in rectangular coordinates. When I was in school I was taught to memorize all of these values, but simply knowing this x - y relationship is more than half the battle. If you understand this, you're better off than I was in college.
Remember in Geometry how we found sine and cosine with SOH-CAH-TOA? Sine=Opposite/Hypotenuse and Cosine=Adjacent/Hypotenuse. Well in the case of the unit circle the hypotenuse (which is always the radius) is always 1, therefore we can ignore it. So sin=opposite, cos=adjacent, or sin=y, cos=x.
| Circle Diagram: Unit Circle & Evaluate Trig Functions - Mr. Gais |
Let's look at 30°. Notice it is further in the x direction than the y direction. We see (√3/2, 1/2). Notice √3/2 is a larger quantity than 1/2, and in the y direction it appears to be halfway up the circle, as we would expect.
Let's look at 45°. This forms a 45°-45°-90° isosceles triangle, so the x and y values are the same! It happens to be (√2/2, √2/2), which is the only other number you need to memorize!
Finally let's look at 60°. This angle is very similar to 30°, but the x and y values are switched, giving us (1/2, √3/2).
The angle 90° is much like 0°. There is no x value, and the y value is simply 1, because it is the radius going straight up in the y direction touching the very top of the circle, giving us the point (0,1).
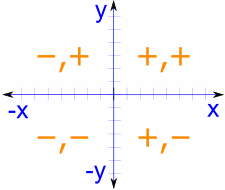
Now that we have these values, we can easily illustrate the rest of the unit circle by placing negative signs in the appropriate places. In the 2nd quadrant, the x value is negative, but the y value stays positive. In the 3rd, both are negative; in the 4th, x is positive and y is negative.
 |
| Quadrants: MathIsFun.com |
Q1: (+,+)
Q2: (-,+)
Q3: (-,-)
Q4: (+,-)
That's all there is to it! We will practice soon with reference angles, but let's do a quick example ahead of time.
Find the unit circle values for 225°. Let's think for a moment.
225° ends with a 5. Surely our best guess would be that it is a reference angle of 45°, since 225° isn't divisible by 30° or 60°. If we visualize it, we rotate counterclockwise starting at the angle 0.
| Image from http://math.stackexchange.com |
180° is halfway around the circle. 225°-180° = 45°. If we go 45° further along the circle, we arrive in the 3rd quadrant with a 45° reference angle. The unit circle value for a 45° angle is (√2/2, √2/2). Since we are in the 3rd quadrant, both values are negative, thus our answer is:
(-√2/2, -√2/2)
As long as you know how far from 0 or 180 the angle is, you can easily find its unit circle values.
For those who like to use their hands to help visualize, there is an amazing trick that makes learning the unit circle as easy as counting 1,2,3; literally. YES you can use this during a test! Here's how:
Left Hand Trick - https://www.youtube.com/watch?v=LE6dmczMc68
Sources:
Gais, J. (n.d.). 2.0 - Unit Circle & Evaluate Trig Functions - Mr. Gais. Retrieved September 28, 2015, from https://sites.google.com/site/mrjgais/Home/trigonometry/unit-circle
Pruitt-Britton, M. (n.d.). Memorizing the Unit Circle Using Left Hand Trick. Retrieved September 28, 2015, from https://www.youtube.com/watch?v=LE6dmczMc68
Rajpoot, H. (n.d.). Calculating a Point that lies on an Ellipse given an Angle. Retrieved September 28, 2015, from http://math.stackexchange.com/questions/22064/calculating-a-point-that-lies-on-an-ellipse-given-an-angle
Trig Unit Circle Why? (n.d.). Retrieved September 28, 2015, from https://www.physicsforums.com/threads/trig-unit-circle-why.475575/
Unit Circle. (n.d.). Retrieved September 28, 2015, from
http://etc.usf.edu/clipart/43200/43215/unit-circle7_43215_md.gif